<アクチュアリー1次試験対策>
2019年12月合格目標 オンライン基礎ゼミ&過去問演習
科目詳細 <損保数理>
日本アクチュアリー会一次試験「損害保険数理」の合格を目指す方のためのGW短期集中実践講義のweb配信版です。「損害保険数理」は特殊な科目で、なじみのない方には難しく、実際合格率も高くはありませんが、出題傾向が安定しており、また、解法に特別なアイデアやひらめきを要求する要素が少ないので、対策は立てやすいと言えます。効率の良い勉強法を身につければ、確実な得点が期待できます。
試験の特性に対応し、講義の進め方は各章とも、いくつかの代表的な出題例を示し必要な解法知識を解説します。出題傾向の分析と、頻出問題を多くカバーすることにより、科目の全体像を理解していただき、短期合格への道をご案内します。
対象者
- 「損害保険数理」科目の基本期・中級レベルの知識習得を目指す方
※ 期待値や密度関数など、確率の基礎概念になじみのない方は、弊社オンライン数学受講後からの同・損害保険数理 受講を強くおすすめします。
講義項目
第1回 緒論 「損害保険数理」合格をめざすには
(1)出題範囲と過去問の傾向
(2)目標設定・合格へのプランニング
キーポイント解説・過去問演習①
『損数』序章 確率・統計の予備知識 (基礎概念、最尤法、条件付確率等)
※「数学的予備知識を網羅する」ものではなく出題との関連のみ解説。
『損数』第1章 損害保険料率の基礎知識 (損害率分析、営業保険料の構成など)
『損数』第2章 クレームの分析 (複合分布、複合ポアソン分布、パラメータ推定等)
第2回 キーポイント解説・過去問演習②
『損数』第3章 経験料率 (信頼性理論、ベイズ方法論、ビュールマンモデル)
『損数』第4章 クラス料率 (ミニマムバイアス法、一般化線形モデル)
『損数』第5章 支払備金 (チェインラダー法、ボーンヒュッター・ファーガソン法)
第3回 キーポイント解説・過去問演習③
『損数』第6章 積立保険 (保険料、払戻積立金)
『損数』第7章 保険料算出原理 (指数原理、エッシャー原理、ワンの原理等)
『損数』第8章 危険理論の基礎 (確率過程、ルンドベリモデル)
第4回 キーポイント解説・過去問演習④
『損数』第9章 再保険 (比例式、ELC、ストップロス等)
『損数』第10章 リスク評価の数理 (極値理論、VaR、TVaR、ケンドールのτ、コピュラ)
積立保険(補講)
結論 科目全体像の振り返りと学習指針
(1)広く浅く⇔深く狭く
(2)合格水準を意識した学習
使用テキスト
配付資料
講師作成の講義レジュメを当日配付します。
使用テキスト(ご持参)
本セミナーで用いる書籍です。各自ご持参してください。
『損保数理』 日本アクチュアリー会 テキスト(『損数』で略記)
小暮雅一、東出純(著)『例題で学ぶ損害保険数理 第2版』共立出版、2016年(『例題で損数』で略記)
https://www.amazon.co.jp/dp/4320111524/
https://books.rakuten.co.jp/rb/14123083/

使用過去問(ご持参)
平成27~29年度の第1次試験過去問題集「損保数理」を、以下サイトよりダウンロード・印刷してお手元にご用意ください。 http://www.actuaries.jp/lib/collection/index.html
※「損保1」「損保2」と記載のあるものは第2次試験のものとなりますので、ご注意ください。
電卓(ご持参)
試験で認められている電卓を各自ご持参してください。
参考サイト)公益社団法人 日本アクチュアリー会 2018年度 資格試験要領
http://www.actuaries.jp/examin/2018exam/2018-H.html
※「7.試験会場で使用可能な電卓について」参照
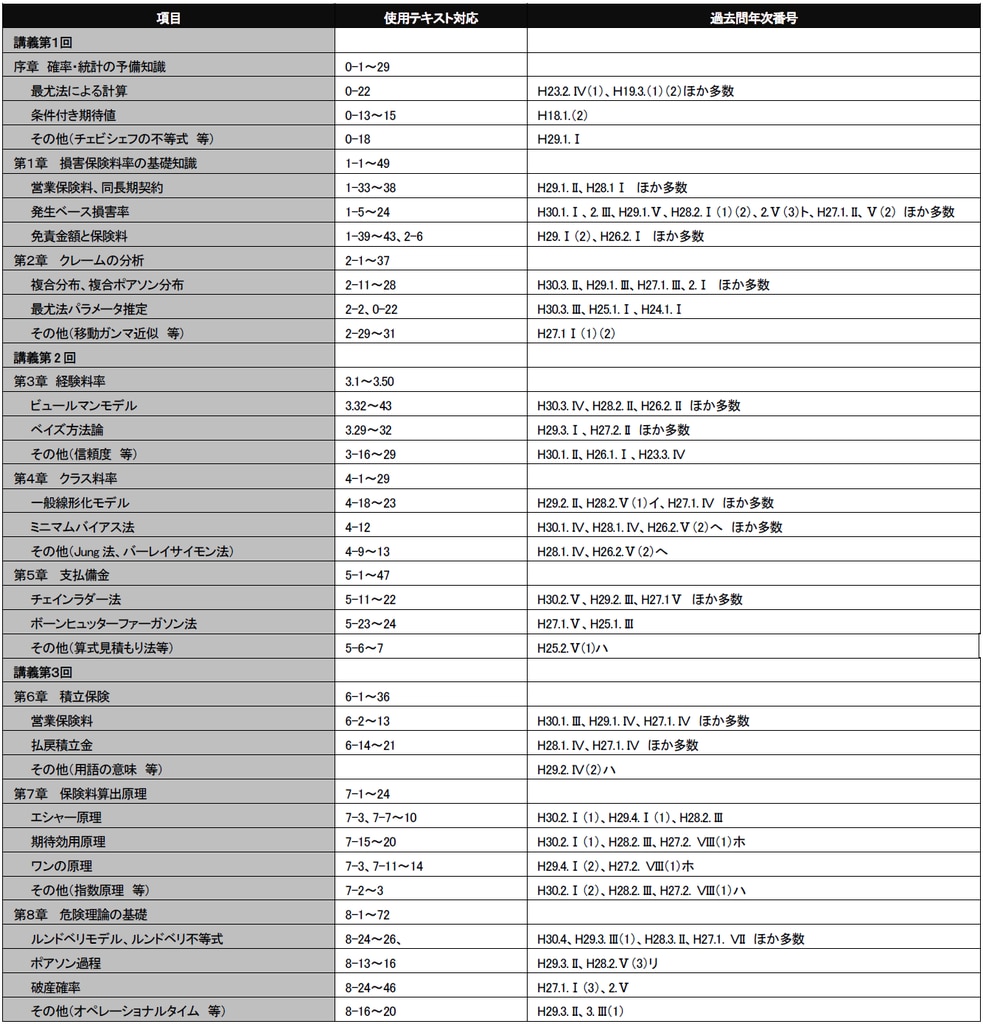
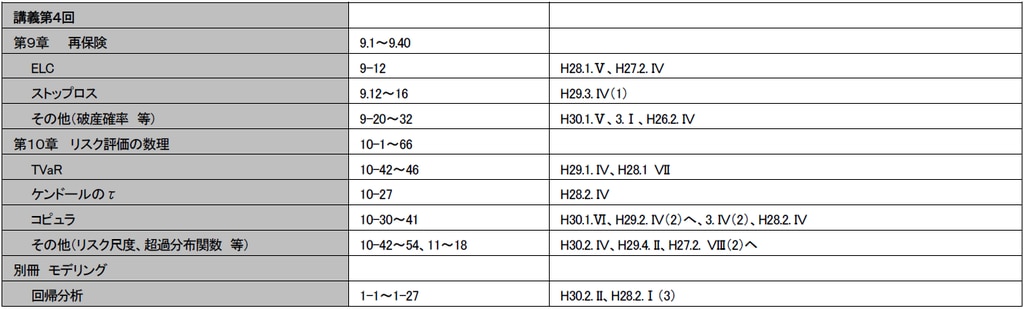
過去問分析
教科書の各章から、満遍なく出題され、とくに第1章~第9章は、ほとんどの年度で何らかの問題が出ています。 したがって、合格には、各章の内容を一通りカバーしておく必要があります。一方、章ごとに中身を見ると、ビュールマンモデルやチェインラダー法など、過去に高い頻度で出題されている項目があります。本講座では、重要な頻出項目を選んで解説しましたので、これらはよく理解し問題演習を繰り返しましょう。一方頻度の少ない項目は、頻出項目をマスターし余力がある場合に取り組むのがよいでしょう。数値の選択肢は、均等間隔の10通りから「最も近い」値を選ぶものがあります。正解には端数処理等の細部まで、十分注意が必要です。題意の定式化に洞察力が要求されるもの、加えて計算力も必要なものなど、「骨のある」問題がある一方、少数ですが、定義や用語の意味を知っているだけで解ける問題もあります。
はじめに全体に目を通し、やさしい問題が時間切れ未着手にならないようにしましょう。
講師紹介

星野 明雄 氏
日新火災海上保険株式会社 顧問
※講師のご所属が変更になりました(2019.04.01)
1985年 東京大学理学部数学科卒。在学中n×n×nルービックキューブの一般解を発表。
1988年 日本アクチュアリー会正会員(FIAJ)。
1995年 ペンシルバニア大ウォートン校卒(MBA)。
1997年 自動車保険・人身傷害補償開発。損害保険上級講座 講師。
ERMA Bali International Seminar on Enterprise Risk Management Panelist。
恐竜研究で独自の「ブラキオサウルス短腕説」を唱える。
オンライン講座 視聴期間・受講料
科目単価:48,000円(税込)
視聴期間:お申し込み完了後~2019年12月31日(火)23:59
<受講希望の方へお願い>
お申し込み前に、テスト視聴ページより推奨環境と動画の再生可否を必ずご確認ください。
■ テスト視聴ページ:https://deliveru.jp/pretest5/
■ ID(ユーザー名):livetest55
■ パスワード:livetest55
お申し込み
▼損保数理(単科目)に申し込む
| アクチュアリー講座TOP | 数学 | 損保数理 | 生保数理 |
Copyright © 1999-2019 Seminar Info Co.,Ltd. All rights reserved.